JSCE Paper Award 2015
Establishment of Coupled Analysis of Interaction between Structural Deterioration and Reinforcement Corrosion by Salt Damage
PDF Version
	Mika SUZUKI	Taisei Corporation
	Naoyuki FUKUURA	Taisei Corporation
	Tsuyoshi MARUYA	Taisei Corporation

T he limit state of durability verification of a reinforced concrete (RC) structure should be corrosion cracking, not the onset of steel corrosion in concrete. It is becoming increasingly important to predict the structural performance of RC structures after the onset of corrosion-induced cracking on a long-term basis. That is, an analysis method that can predict structural performance is required.

We developed a coupled analysis of the interaction between structural deterioration and reinforcement corrosion by salt damage (Figure 1). Nonlinear structural analysis of the RC member is used for structural deterioration. The chloride ion diffusion model and a model of micro-cell and macro-cell corrosion are used for the reinforcement corrosion. For reinforcement corrosion, we incorporated the distribution of macro-cell corrosion current density.

The chloride ion diffusion model for cracked concrete is set up according to Djerbi’s method. If a single crack occurs in one element and the width of the crack is obtained by multiplying the tensile strain by the average crack width, then the diffusion coefficient for the finite element can be calculated as shown in Equation (1).

where D₀ is the diffusion coefficient of the non-cracked concrete, D_cr is the coefficient of diffusion through the finite element with the crack, α_d is the proportional increase in the diffusion coefficient due to the crack, d_cr is the proportional increase in the diffusion coefficient of the cracked part compared with D₀ (a function of ω), ω is the crack width (=ε ·l), ε is the orthogonal direction to the crack tensile strain (>0), and l is the average length of a finite element ( V^1/3, where V is the volume of a finite element)
Corrosion expansion is modelled as a radial increase in the steel volume under a confining pressure (Figure 2). The steel bar expansion strain ε_fix, which is caused by corrosion expansion under a confining pressure, is the increase in volume V of a unit length of steel.

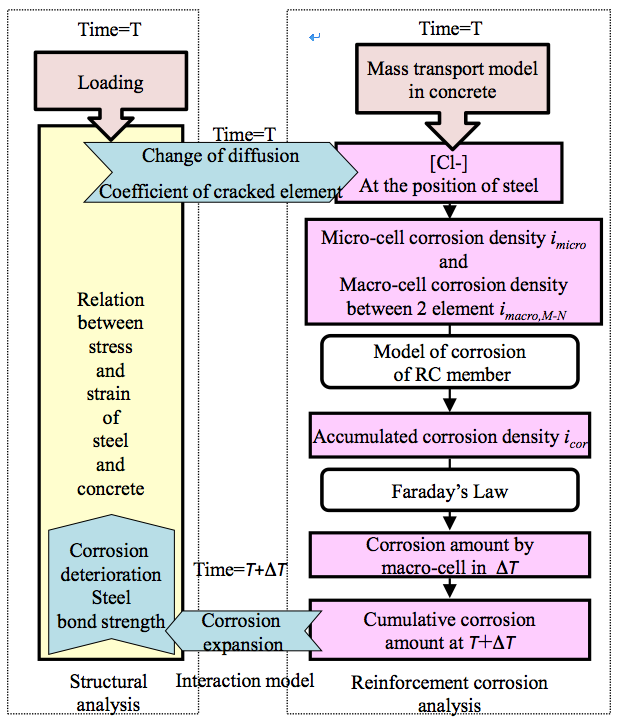Figure 1. Flow diagram of coupled analysis

The macro-cell corrosion is calculated using internal polarization curves and external polarization curves. The macro-cell corrosion between two elements (element M, N) of steel in concrete is shown in Figure 3 under the condition that the area of the anodal element equals the area of the cathodal element.

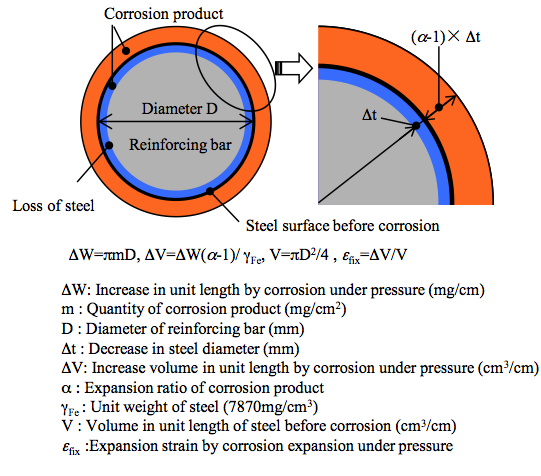Figure 2. Model of corrosion expansion

Figure 3. Macro-cell corrosion between two elements (element M, N) of steel in concrete

Current density i_g,M―N at that time is the current density when the potential difference between the external cathodal polarization curve (i_app,c,M，E_c) and the external anodal polarization curve (i_app,a,N，E_a) is equal to the potential difference ΔE_M－N of the concrete resistance between element M and element N (Equation 2).

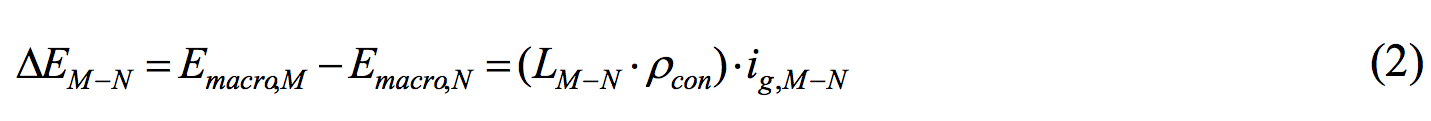When a reinforcing bar is modelled with a plural divisional element, the influence of the ratio of the cathodal area and the anodal area is considered. The distribution diagram of macro-cell corrosion current density β is set, and a macro-cell corrosion current between the cathode and each anti-anode from a certain cathodal element is distributed into each anti-anodal element.

The macro-cell corrosion current density of a certain anodal element (N_i), when n unit anodal elements exist for a certain cathodal element (M), is shown in Equation (3). The distribution diagram β_M－Ni is set by Equation (4). The introduction of such a distribution diagram is not strictly expressed the distribution of the macro-cell corrosion current density, which occurs between plural elements in a real situation. It was thought that the model adjusts to the real situation, such as a higher chloride ion concentration of the anodal part, a closer distance between the cathodal part and anodal part, a bigger cathodal area or a smaller anodal area, or a larger quantity of corrosion product per unit area.

All of the corrosion current densities in element K of the steel in an RC member are illustrated in Figure 4 and calculated using Equation (5). The corrosion current density is the micro-cell corrosion All of the corrosion current densities in element K of the steel in an RC member are illustrated in Figure 4 and calculated using Equation (5). The corrosion current density is the micro-cell corrosion current density i_micro,K plus the macro-cell corrosion current density between element K and the other elements when element K is the anodal element, minus the macro-cell corrosion current density between element K and the other elements when element K is the cathodal element.
The time increment of the corrosion quantity of element K, which is shown in Equation (6), is calculated using Faraday’s law.

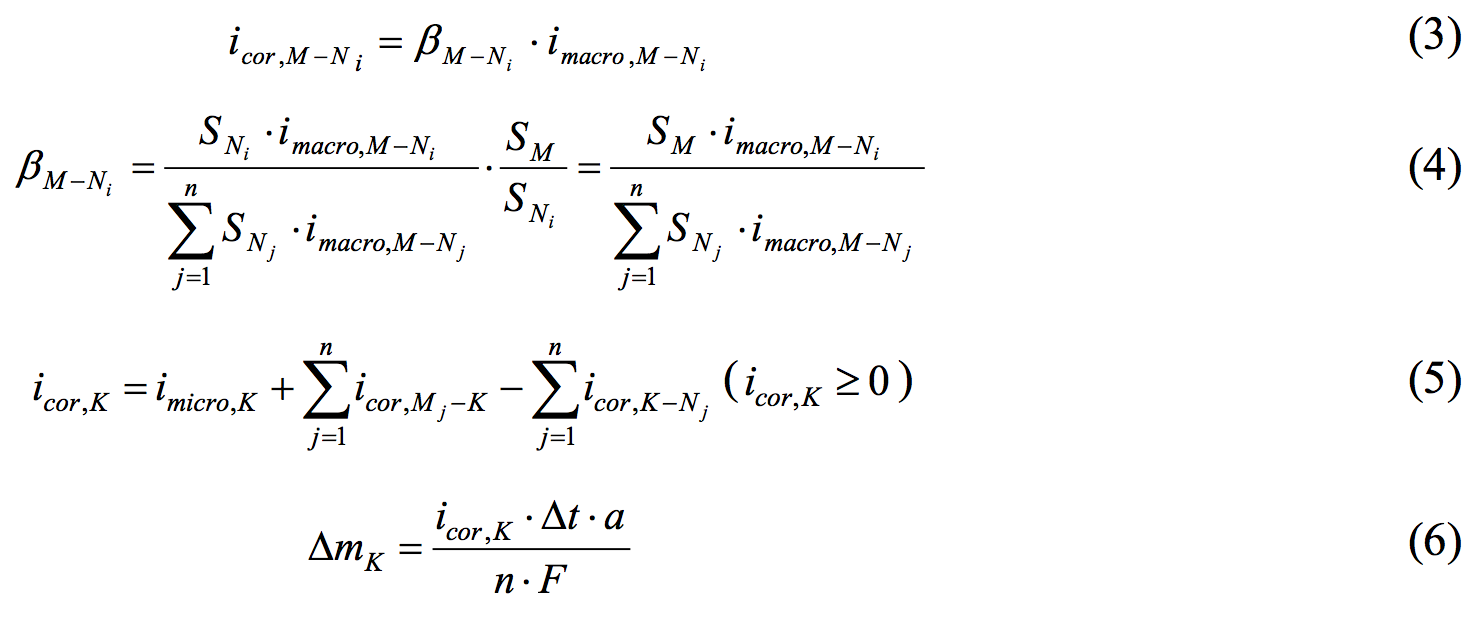where i_cor,M－Ni is the macro-cell corrosion current density between element M and element Ni of the steel in the RC member (A/cm²), β_M－Ni is the distribution diagram of the macro-cell corrosion current density between element M and N_i, S_M is the surface area of element M (cathodal part)(cm²), S_N is the surface area of element N (anodal part)(cm²), i_cor,K is the total corrosion current density of element K (A/cm²) ,Δ_mK is the time increment of the corrosion quantity of element K(g/cm²), Δ t is the time increment(s), a is the atomic weight of iron (55.845), n is the equivalent of dissolved iron ion (2 mol eq), and F is the Faraday constant (96500 C/mol eq).

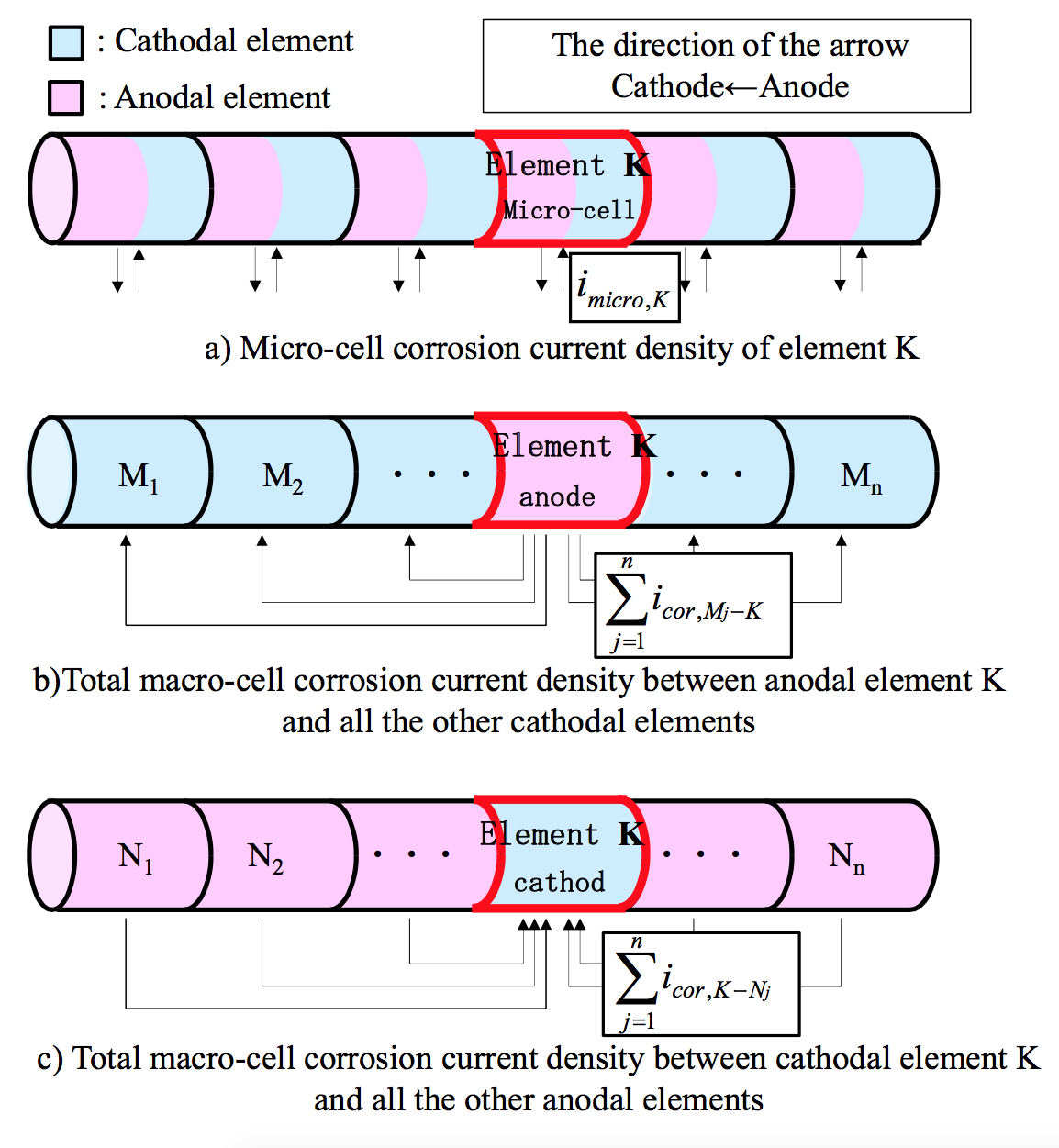Figure 4. All corrosion current densities in element K of steel in an RC member

The proposed analytical method is validated through dry-wet cyclic tests with a salt solution to simulate macro-cell corrosion due to an inspection of the corrosion amount after corrosion cracking.
The experimental setup of the specimens is illustrated in Figure 5.
Table 1 shows the FEM analysis cases. Figure 6 shows the 1/2-scale model used for analysis, which was adopted in consideration of the sectional symmetry and exposure conditions. The proportional increase in the diffusion coefficient of D₀ in the cracked part, d_cr, was set according to Model 1 and Model 2 (Figure 7).

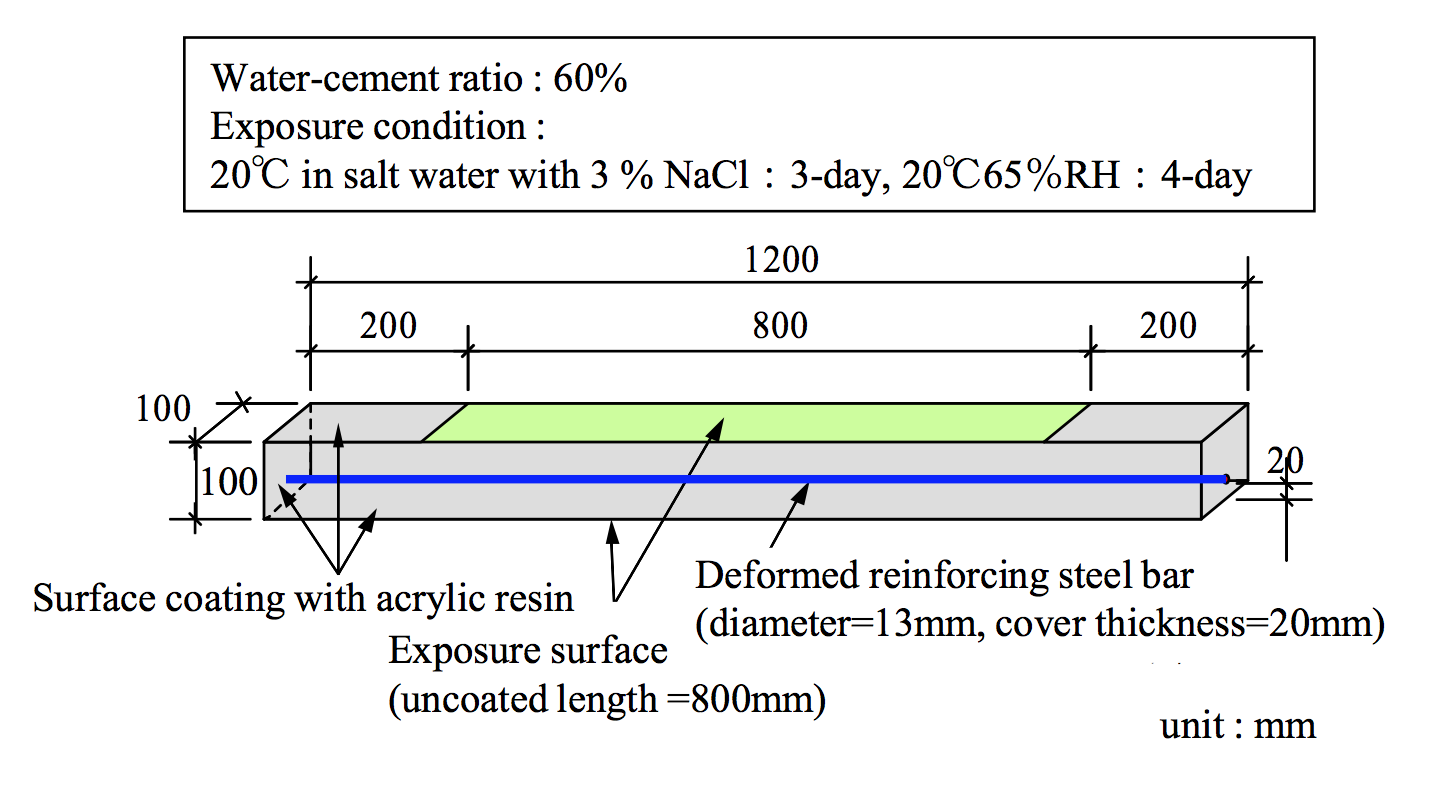Figure 5. Overview of experiment

Table 1. Analysis cases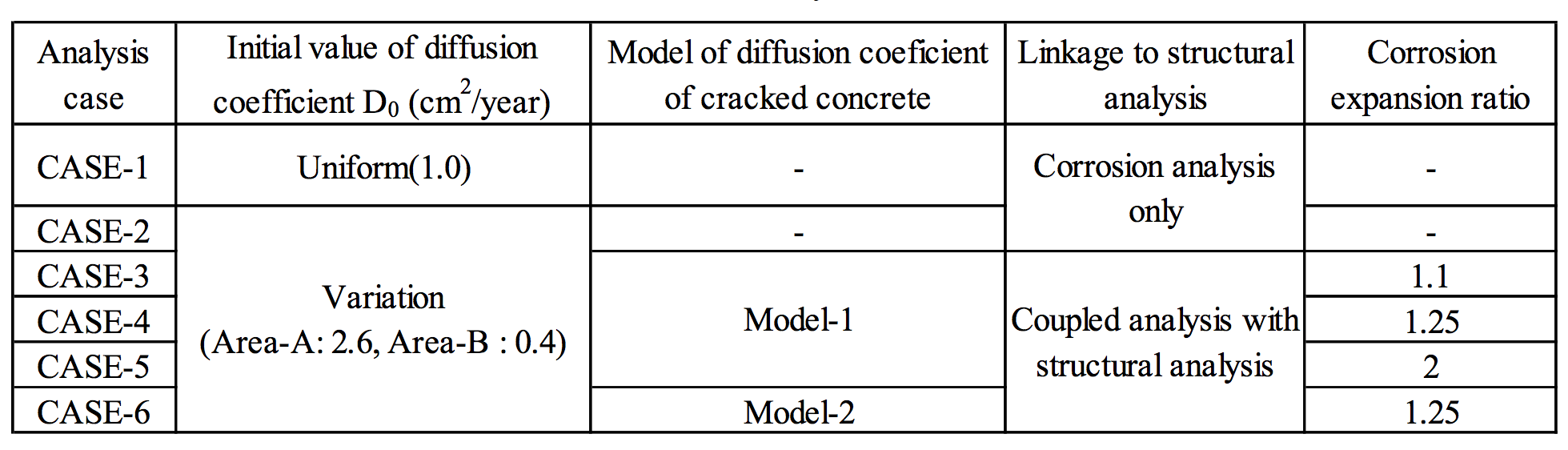

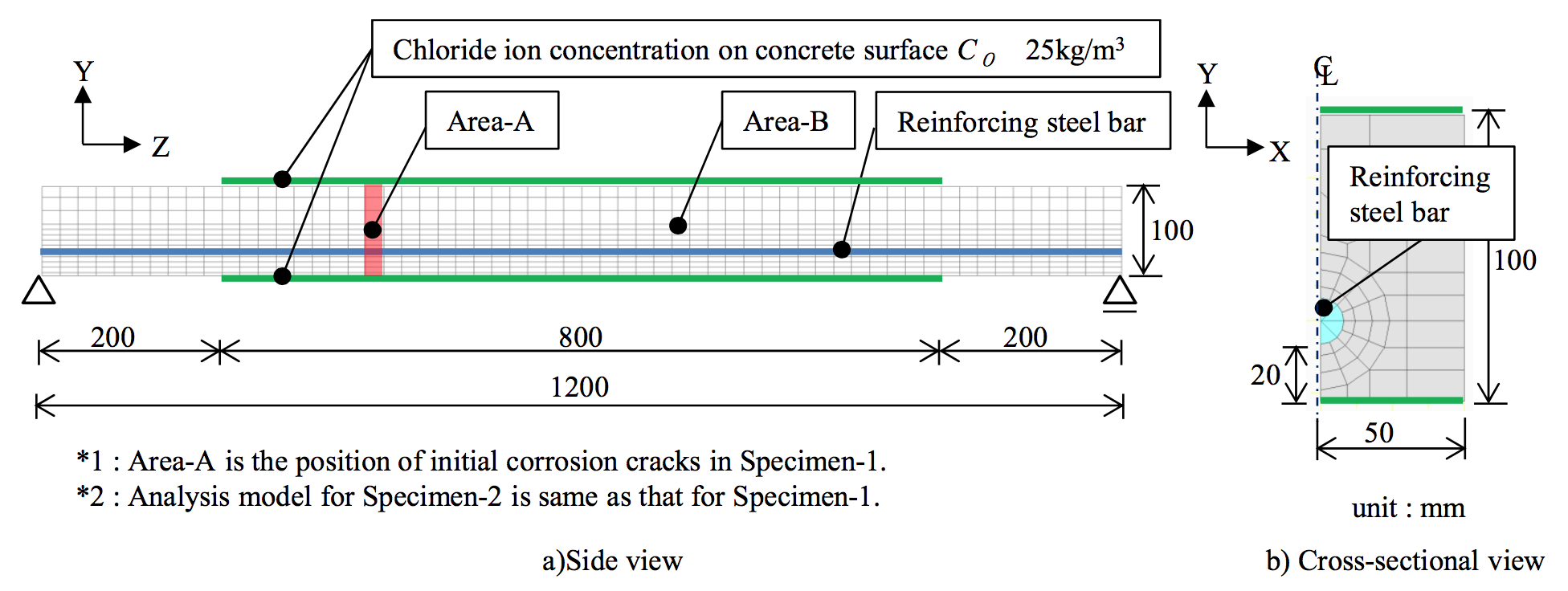Figure 6. Analysis model

Figure 8 compares the chloride ion concentration in the experiment and analysis. For Specimen 2, the position of the analysis was adjusted by 100 mm to match the position of the corrosion cracks in the experiment with Area A in the analysis in Figure 6. Cases 2 to 6, which considered the non-homogeneity of initial diffusion coefficient D₀, reproduced the experimental trend.

Figure 9 compares the amount of corrosion in the experiment and the analysis. The area of increased chloride ion concentration that was extended due to the onset of corrosion cracking in Cases 3 to 5, which are the coupled-analysis cases using Model 1 for the diffusion coefficient of the cracked concrete. The anode area of the macro-cell corrosion and the corrosion area also expanded. The analysis results agree to the experimental trend.

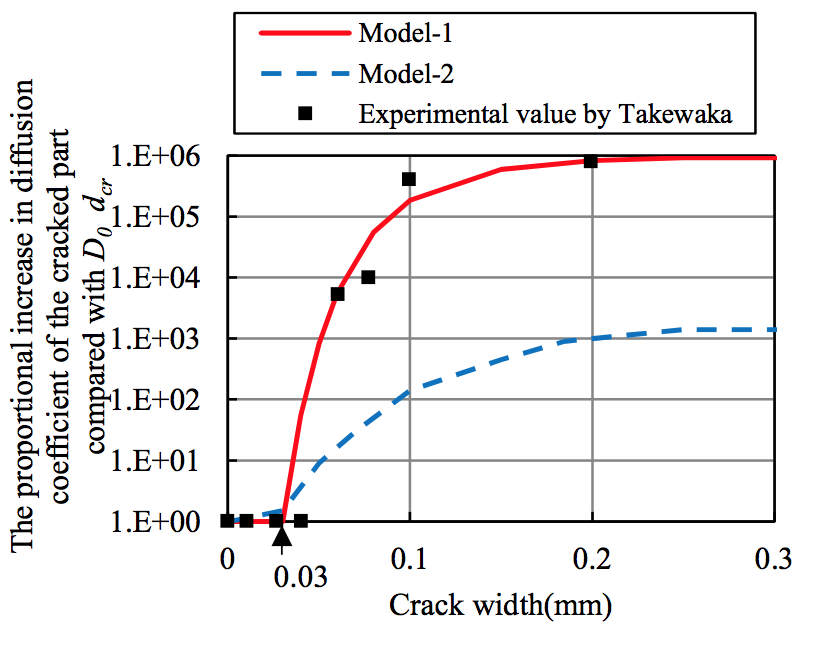Figure 7. Proportional increase in the diffusion coefficient of the cracked part

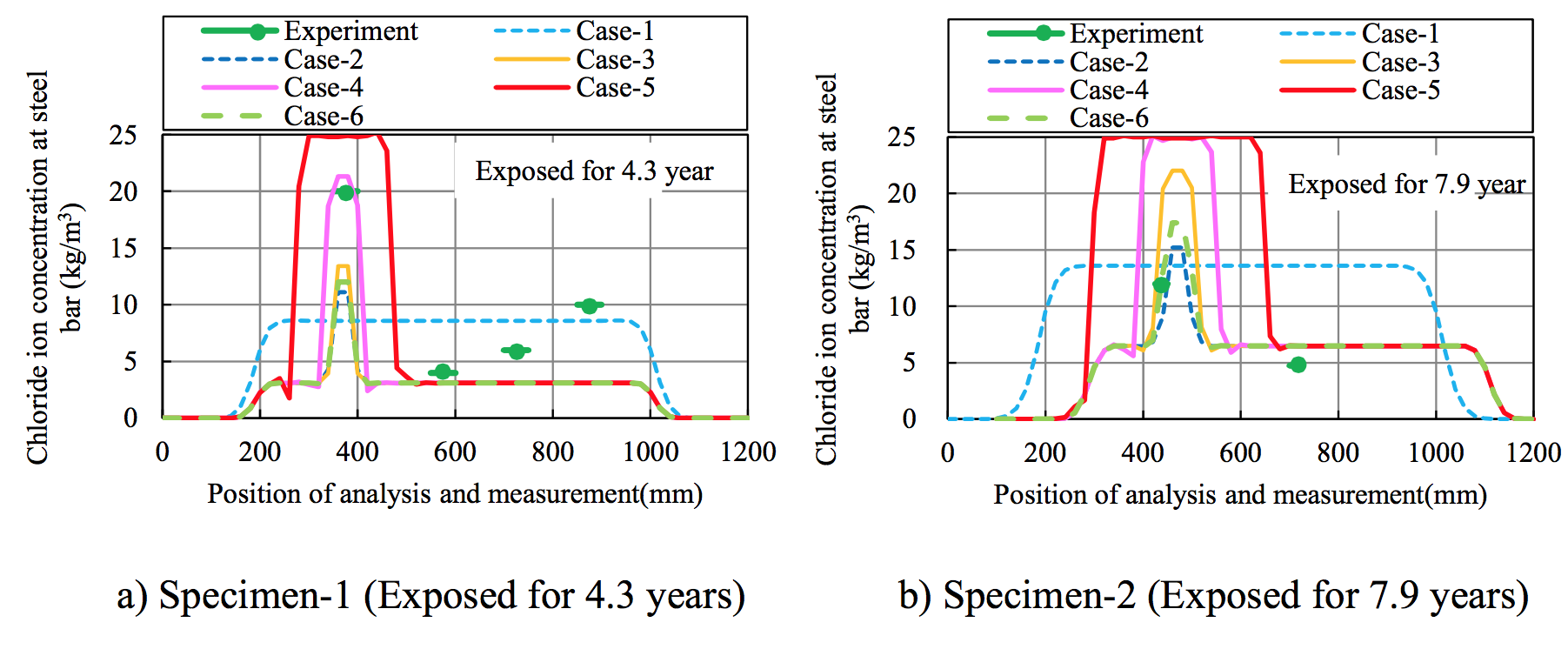Figure 8. Comparison of chloride concentrations in experiment and analysis

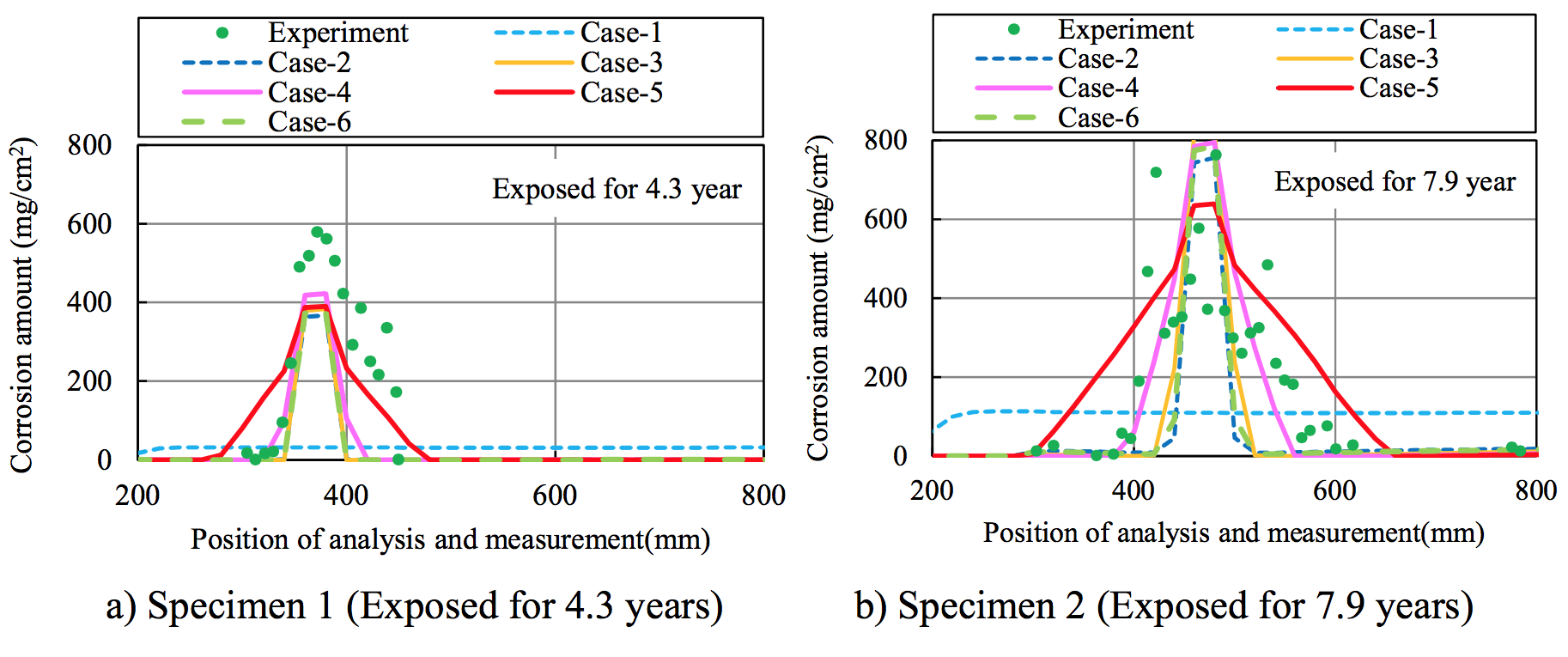Figure 9. Amounts of corrosion in experiment and analysis