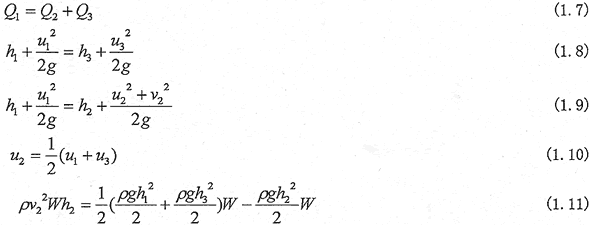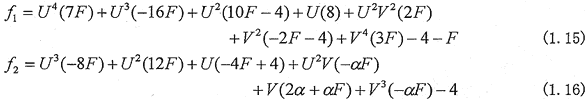1.急勾配河川における氾濫流とこれに伴う土砂堆積
金沢工業大学工学部
山坂昌成
1.1 まえがき
洪水時に、河岸の浸食や越水に起因して堤防が決壊すると、河道内の水は堤内地に氾濫し、人的、経済的などさまざまな甚大なる被害が生じる。低平地の氾濫は、比較的頻繁に見られるが、その流れの速度や水位上昇速度が比較的緩やかであるため、人的被害は少なく、経済的な被害も浸水そのものによるもの(濁水につかる)が大部分で、、構造物の破壊などの被害は比較的少ない。これに対して、急流河川では、氾濫流の流速は家屋などの構造物に衝撃力をもたらすほど速く、氾濫流が一気に広がるため、人的被害をなくすためには精度の高い氾濫予想に基づいた早めの避難対策も必要である。また、急流河川では、洪水時に大量の土砂が流れ、堤防の決壊を伴う氾濫では、土石の流出による構造物への衝撃、氾濫域への土砂堆積による氾濫流況の変化が、予期せぬ地域への被害を増大させる可能性も生じる。
このように、急流河川の氾濫被害は甚大であることから、堤防は破堤を絶対に生じないような強固なものにする必要がある。しかし、堤防の全延長を一気に改修することは予算的に困難であるため、氾濫による被害を定量化し、重点的に堤防強化の改修を行う地点を選定する必要が生じる。
本共同研究は急流扇状地河川の常願寺川を対象河川として行われたものであるが、常願寺川のある地点で破堤した場合の被害の定量化については、筆者の能力を超えた範囲であると判断し、実験規模で生じる土砂を含む急勾配水路の氾濫流の特性と、その定量的な扱いについて検討することにした。
1.2 実験装置および実験概要
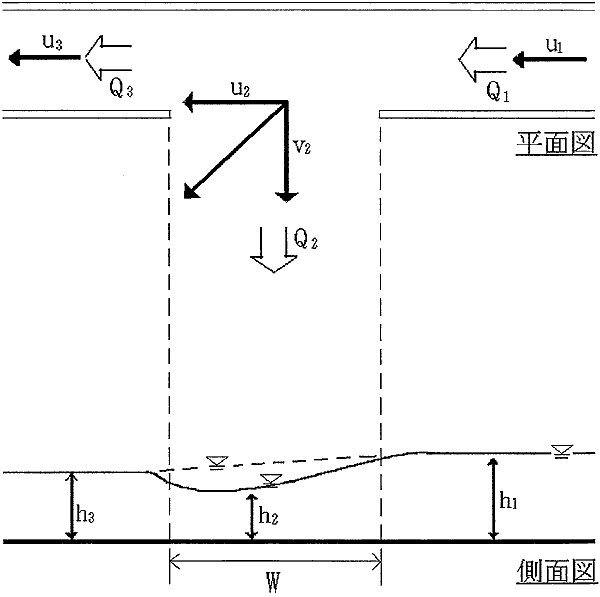
氾濫流の室内模型実験装置は、金沢工業大学内の水理実験室に設置され、氾濫域は水路の勾配と同一の縦断勾配を有する平板から構成される。水路は図-1.1に示すように、内幅B=15cm、高さ15cm、長さ387cmで、側壁は透明アクリル板、底面はベニヤ板製である。長さ方向の水路中央付近の左岸壁に開口幅W=12.7cmの開口部を設け、ここから水路を流れる水が氾濫する。氾濫域は幅100cm、長さ200cmのベニヤ板で構成され、水路との接続部以外の縁下には雨樋が設置され、氾濫流量を下流水槽に流すとともに、氾濫流量を1つの容器に受け止め、その体積を測定することにより、氾濫流量を測定できるような仕組みになっている。氾濫流量が大きい場合、雨樋から下流水槽につながる配水管の容量の不足から雨樋からの溢水が見られたので、配水管は雨樋の途中3ヶ所からの3本を設置した。なお、氾濫域の平板にはビデオ撮影、写真撮影用の座標認識のため、10cm間隔の格子線が引かれている。
水路および氾濫域は一体化して単管パイプ製の台に設置し、単管パイプの接地面にジャッキベースを取り付けることにより、全体の勾配を調節できるようにしている(写真-1.1参照)。勾配は、それぞれ、急勾配である1/100と1/300の2種類を設定し、それぞれについて、流水のみの実験(A,Bシリーズ)と水路内に平均粒径d=1.15mmの砂を流した、土砂を含む流れの実験(C,Dシリーズ)とを行った。流水のみの実験では、通水を開始し、流れが安定した後に、下流端流量と氾濫流量を測定し、水路内の水深分布、氾濫出口の水深を測定した。氾濫域の水深については、場所によっては水深が極めて小さいこと、測定範囲がかなり広範囲にな
る等の理由から、測定を行っていない。氾濫出口の流速については、ピトー管による測定、電磁流速計での測定を試みたが、水深が小さい上に流速が速いため、キャビテーション域に空気が混入し、信頼できるデータは得られなかった。これに代わる方法として、水面に浮かぶ発泡スチロール粒子の痕跡から、氾濫出口の表面流速の概略値を求めた。用いた発泡スチロールは直径約8mmの白色球で、撮影は露光時間を1/60または1/30秒にしたデジタルスチールカメラで行った。
土砂を含む氾濫流れの実験では、全流量、氾濫水量の測定に加え、氾濫開始後1分、2分、3分、5分に通水を止めて氾濫域への土砂堆積高さを測定し、これを測定した時とほぼ同一の堆積形状のもとで、氾濫流の表面に流した発泡スチロール球の軌跡をデジタルビデオカメラで
上方から撮影したビデオ映像より、流況を読み取った。撮影時間間隔は1/60秒で、この間の移動距離から表面流速を測定できる。ただし、発泡スチロール球を氾濫域に均等に散布するのは困難で、水路内に流した発泡スチロール球が自然に氾濫域に流出する様子を撮影したので、球の存在する位置は、比較的氾濫の主流域近くであると考えられる。堆砂実験では、流速測定のための時間が制限されるため、流況については、発泡スチロールの1回散布から粒子軌跡を求めるにとどめた。
1.3 流水のみの氾濫実験
表-1.1に流水のみの氾濫実験における実験条件と氾濫流量についての実験結果を一覧にして示す。Aシリーズは勾配が1/100、Bシリーズは勾配が1/300の条件で行った。図-1.2(a),(b)に各実験で得られた総流量と氾濫流量の関係を棒グラフで示す。Aシリーズ、Bシリーズともに、総流量が増えると氾濫流量が増加する傾向にある。総流量に対する氾濫流量の割合が、総流量によってどのように変化するかを図-1.3(a),(b)に示す。それぞれのシリーズで氾濫流量の割合はほぼ一定であるが、総流量が増えるほど氾濫割合が若干増える傾向にある。また、水路勾配の違いに着目すると、勾配の緩いBシリーズの方が氾濫割合はやや大きい。
氾濫流量は、本川内流量より、むしろ本川の推移に支配されると考えられるので、本川の上流水深と氾濫流量の関係を図-1.4に示す。■がAシリーズ△がBシリーズである。A,Bシリーズともに、氾濫流量は上流水深と深い相関をもち、1本の曲線にきれいにのっているように見受けられる。図-1.3や図-1.4の関係を関数表示して氾濫流量公式を導いても、定性的傾向に一般性が見られるだけで、実験に用いた水路に特有の氾濫流量しか推定できないことになるので、任意の寸法、規模の水路に適用できる氾濫流量の推定法について検討する。
緩流河川においては、横越流量の公式として、しばしば堰の越流量公式や、これをやや改良した方法が用いられる1),2)。これを準用し、
- 氾濫出口で限界水深を取る
- 本川上流の速度水頭を無視して、氾濫出口の水深h2(限界水深)が本川上流水深の2/3となる
- 氾濫流は、本川に垂直な方向に流出する
と仮定すると、氾濫流量Q2は、
から求められる。ここにWは氾濫開口幅である。図-1.4の◆印は、式(1.1),(1.2)で表されるh1とQ2の関係を示す。実測のh1とQ2の関係式は式(1.1),(1.2)の理論曲線と同様の変化の仕方を示すが、大きさに2倍ほどの差が現れている。この原因は、本川上流の速度水頭を無視していることなど、いくつか考えられるが、氾濫出口で限界流となる仮定、流出方向が本川に垂直となる仮定が主要因であると考えられる。前者については、急勾配水路では本川上流川で既に射流となっているのに、氾濫出口で単位幅流量を最大(与えられた比エネルギーのもとで)
勾配1/100| No | 総流中 | 水路流量 | 氾濫流量 | 割合% | 上流水深 | 上流流速 | 上流フルード数 |
| Q1(cm3/s) | Q3(cm3/s) | Q2(cm3/s) | h1(mm) | u1(cm/s) | Fr1 | ||
| A-1 | 935 | 810 | 125 | 13.4 | |||
| A-2 | 1019 | 890 | 130 | 12.7 | 13.84 | 50.78 | 1.38 |
| A-3 | 1687 | 1502 | 184 | 10.9 | 16.02 | 72.61 | 1.83 |
| A-4 | 1921 | 1667 | 254 | 13.2 | |||
| A-5 | 1922 | 1664 | 258 | 13.4 | 21.10 | 62.83 | 1.38 |
| A-6 | 2533 | 2239 | 295 | 11.6 | 23.46 | 74.46 | 1.55 |
| A-7 | 3165 | 2741 | 424 | 13.4 | 28.86 | 75.61 | 1.42 |
| A-8 | 3510 | 3068 | 442 | 12.6 | 29.73 | 81.42 | 1.51 |
| A-9 | 4019 | 3543 | 476 | 11.9 | 29.96 | 92.52 | 1.71 |
| A-10 | 4377 | 3814 | 563 | 12.9 | |||
| A-11 | 4490 | 3969 | 522 | 11.6 | 32.67 | 94.80 | 1.68 |
| A-12 | 4755 | 4089 | 665 | 14.0 | 41.69 | 78.66 | 1.23 |
| A-13 | 5220 | 4578 | 642 | 12.3 | 37.27 | 96.58 | 1.60 |
| A-14 | 5710 | 4949 | 760 | 13.3 | 43.43 | 90.66 | 1.39 |
| A-15 | 5920 | 5048 | 872 | 14.7 | 45.49 | 89.75 | 1.34 |
| A-16 | 6009 | 5187 | 822 | 13.7 | |||
| A-17 | 6285 | 5484 | 802 | 12.8 | |||
| A-18 | 6352 | 5455 | 897 | 14.1 | |||
| A-19 | 6679 | 5792 | 887 | 13.3 |
| No | 総流中 | 水路流量 | 氾濫流量 | 割合% | 上流水深 | 上流流速 | 上流フルード数 |
| Q1(cm3/s) | Q3(cm3/s) | Q2(cm3/s) | h1(mm) | u1(cm/s) | Fr1 | ||
| B-1 | 822 | 716 | 106 | 12.9 | |||
| B-2 | 1220 | 1067 | 153 | 12.5 | |||
| B-3 | 1273 | 1093 | 180 | 14.2 | 16.20 | 54.19 | 1.36 |
| B-4 | 1392 | 1206 | 185 | 13.3 | 16.41 | 58.48 | 1.46 |
| B-5 | 2014 | 1734 | 280 | 13.9 | 19.92 | 69.74 | 1.58 |
| B-6 | 2187 | 1864 | 323 | 14.8 | |||
| B-7 | 3015 | 2598 | 418 | 13.9 | 28.24 | 73.65 | 1.40 |
| B-8 | 3666 | 3139 | 527 | 14.4 | 31.82 | 79.45 | 1.42 |
| B-9 | 3738 | 3154 | 584 | 15.6 | 31.49 | 81.86 | 1.47 |
| B-10 | 3795 | 3206 | 589 | 15.5 | |||
| B-11 | 3822 | 3223 | 599 | 15.7 | |||
| B-12 | 3916 | 3318 | 598 | 15.3 | |||
| B-13 | 4078 | 3522 | 556 | 13.6 | 33.00 | 85.22 | 1.50 |
| B-14 | 4140 | 3511 | 629 | 15.2 | |||
| B-15 | 4710 | 3967 | 743 | 15.8 | |||
| B-16 | 4830 | 4099 | 731 | 15.1 | 40.02 | 83.24 | 1.33 |
| B-17 | 5278 | 4501 | 777 | 14.7 | 39.67 | 91.76 | 1.47 |
| B-18 | 5670 | 4915 | 755 | 13.3 | |||
| B-19 | 58551 | 4939 | 912 | 15.6 | |||
| B-20 | 6036 | 5218 | 818 | 13.6 | 43.27 | 96.20 | 1.48 |
| B-21 | 6136 | 5154 | 982 | 16.0 | 45.92 | 92.15 | 1.37 |

(a) Aシリーズ
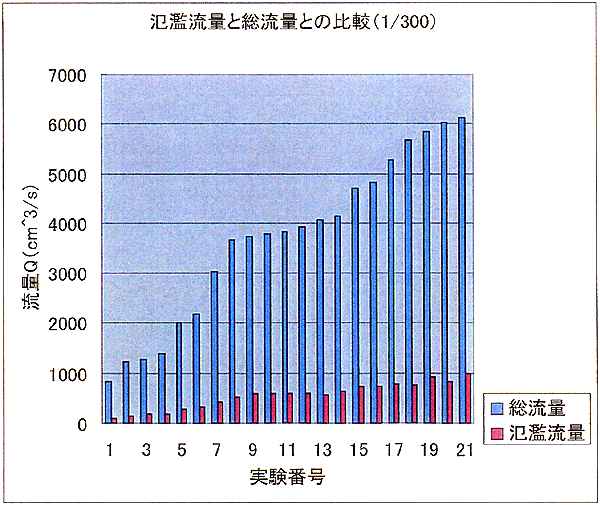
(b) Bシリーズ
図-1.2 総流量に対する氾濫流量の関係

(a) Aシリーズ
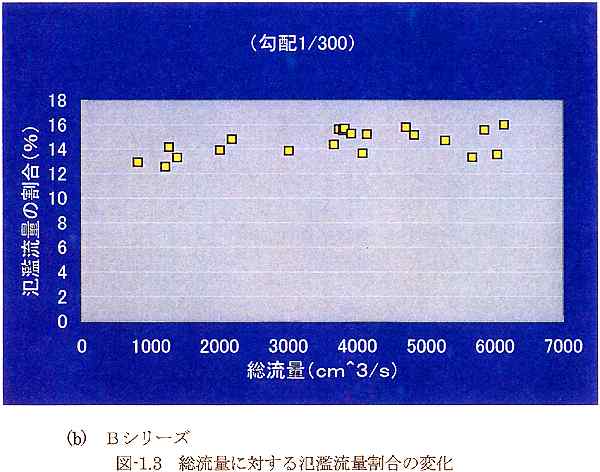
(b) Bシリーズ
図-1.3 総流量に対する氾濫流量割合の変化

図-1.4 上流水深と氾濫流量の関係
とする限界水深をとるという仮定は氾濫流量を大きめに見積もることにつながる。後者については、氾濫出口での流れの方向を本川下流方向から角度θであるとし、流速の絶対値を![]() とすると、
とすると、
![]()
で氾濫流量を推定すべきところを、sinθ=1としているため、大きめの推定値となってしまう。写真-1.2は、氾濫出口の真上から撮影した水表面の発泡スチロール粒子軌跡である。この写真からθ≒40°と読みとると式(1.1)では1/sin40°=1.6倍の推定値を生み出すことになる。こられの要因が相乗して式(1.1),(1.2)では実測値の2倍もの値を推定してしまうと考えられる。
これらを改善すべく、氾濫出口での流向などを考慮した平面二次元流れの準一次元的解析(流下方向・横断方向の速度を考慮するが、その分布は無視)を試みる。扱う水理量は、図-1.5に示すように、本川上流における流量Q1、流速u1、水深h1、下流における流量Q3、流速u3、水深h3、氾濫出口における流量Q2、流速u2,v2、水深h2である。なお、本川幅をB、氾濫出口の開口幅をWとする。これらの水理量のいくつかは従属で、定義式により、
である。ここでQ1、h1を与えて、Q2、Q3を求めるには、h2、h3などを含んだ8個の未知量に対する8個の運動方程式が必要である。式(1.4)〜(1.6)を除いた残りの5個の方程式は、質量保存則(連続式)、エネルギー保存則(ベルヌーイの定理)、運動量保存則から得られる。これらを定式化すると、
となる。運動量の保存則は氾濫出口幅を一辺とする本川内の長方形領域を検査領域として適用し、圧力は領域境界において静水圧分布をするものと仮定している。また、この検査領域の上・下流境界を通しての横断方向運動量輸送を無視し、氾濫出口対岸の圧力は水深h1による静水圧からh3による静水圧へと直線的に変化すると仮定している。流下方向の運動量保存則を式(1.10)で表したのは、これを満足するとき、流下方向の運動量保存則が式(1.8)のエネルギー保存則と等価になるためである。
ここで、
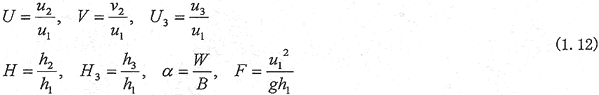
のような無次元化を行い、式(1.4)〜(1.11)を整理すると、
のような、未知量U,Vに関する非線形二元連立方程式が得られる。ここに、
である。式(1.13)〜(1.16)から氾濫出口における無次元流速U,Vが求まると、氾濫出口の無次元水深Hは、式(1.9)を変形した、
![]()
より、氾濫流量比Q2/Q1は、
![]()
から得られる。
式(1.13),(1.14)の非線形二元連立方程式は、ニュートン・ラプソン法3)を用いた繰り返し数値計算で解くことにする。U,Vの第i近似解をそれぞれU(i),V(i)で表すと、i+1次解は、

を満足する必要があるが、
が微小であるという仮定のもとにおいては、式(1.21),(1.22)はTaylor展開されて、
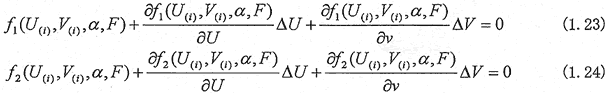
のように近似される。このような展開を用いると、ΔU,ΔVは線形の二元連立一次方程式の解となり、以下のように容易に求められる。
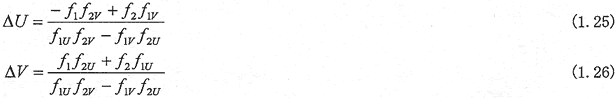
上式でfの第2の添え字が付くものは、これによるfの偏導関数であることを示す。式(1.21),(1.22)を用いてU(i+1),V(i+1)を求め、この計算を繰り返すことにより、ΔU,ΔVがある設定値より小さくなった段階で解が収束したとみなして計算を終了させる。
図-1.6は本研究の各実験条件に対して、F(上流のフルード数の2乗Frl2)と氾濫流量比の関係を示す。理論値では、氾濫開口幅と水路幅の比は実験値での値α=12.7/15=0.85の一定値を与えている。図-1.6では図-1.4に比べ氾濫流量の精度が上がり、フルード数が大きいほど氾濫流量比の変化の状況が、実測値をよく表現している。フルード数が大きいほど氾濫流量比が小さくなるのは、フルード数が大きいほど慣性力の影響で直進性が増し、横断方向への氾濫が抑制されるためであると考えられる。ここでも、推定値が実測値を上回るものの、その差は図-1.4
に比べてかなり小さくなっている。不一致の主な原因は、検査領域の上・下流境界を通しての横断方向運動輸送の無視、氾濫出口では水深が流下方向に大きく変化するのにh2という1つの値で代表させている点にあると思われる。後者については、αの値が小さくなるほどその影響は少ないと思われる。氾濫流量の推定精度を向上させるためには、これらの点を改善する必要がある。
実験では氾濫流量に及ぼす開口幅の影響を調べることができなかったが、この影響を計算値で調べてみる。図-1.7に、単位幅流量で表した氾濫流量比と、開口幅−水路幅比の関係を示す。単位幅の氾濫流量比は
![]()
から得られる。Fr>1である射流の場合は、図-1.6に示したように、同一の開口幅比ではFrが小さいほど氾濫流量比が大きくなる。また、開口幅比が増大するほど、氾濫流量比は若干減少する。これは、Wの増加で氾濫流量が増大するにつれて下流の水位が低下するため、開口単位幅あたりでは氾濫流量が若干減少することになると考えられる。開口幅が1.5を越える領域では単位幅の氾濫流量比がほぼ一定(氾濫流量Q2が開口幅Wに比例)となるが、先に述べた理由により、この領域への適用の妥当性は保証できない。
参考のために、Fr<1の常流の場合(Frl2=0.8の◆印)を示したが、Fr<1の常流では、開口幅比が増加するにつれて単位幅の氾濫流量比も増加する。これは、計算上、本川の水面形が射流の場合と逆の変化を示し、流量の少なくなる下流で水位が高くなるためであると考えられるが、境界条件の設定などの制約から、本解析法を常流状態の流れに適用することは推奨できない。
1.3 土砂を含んだ氾濫流の堆砂実験
前節と同様の実験条件で、水路内に粒径が約d=1.15mmの砂を敷き、通水中、水路内の砂がなくならない程度に砂を手動で上流端より供給した氾濫流の堆砂実験条件を表-1.2に示す。通水開始から1分後、2分後、3分後、5分後に通水を停止し、堆積高を鋼尺を用いて測定した。測定位置は、氾濫域の平板に描かれた10cmメッシュの格子点を基準に5cm間隔とした。最終の堆積状況測定が通水5分後と短いのは、氾濫域が狭く、それより長時間後では砂が雨樋まで到達して、水がうまくはけなくなってしまうのと、そこでの境界条件が大きく変わってしまうため、この時間で実験を打ち切ったことによる。
通水後1分、5分の堆積等高線図から、流量の違いによる堆積形状の違い、勾配による堆積形状の違いを調べてみる。図-1.8は、勾配が1/100のCシリーズについて、流量が約1100cm3/sの場合((a),(b))と流量が約600cm3/sの場合((c),(d))の1分後と5分後の堆積分布図を示す。流量が小さい場合は、堆積形状が下流方向に細長い形状となり、氾濫出口付近から堆積が始まっている。これに対して、流量が大きい場合は堆積形状は横方向にも広がり、氾濫出口付近にはほとんど堆積していない。このような堆積形状は、流量が大きい場合、氾濫流の流速が特に開口部付近で大きく、流れが横方向に広がって、その後流速が減少する流れの状況に対応している。図-1.9は同様に勾配がやや緩くなった1/300の場合について、流量の違いによる堆積形状の違いを示す。流量の違いによる堆積形状の違いの特性は、勾配が1/100の場合と大きくは変わっていない。
| 総流料 (cm3/s) |
水路流量 (cm3/s) |
氾濫流量 (cm3/s) |
時間 | 水路水深(cm) | 氾濫出口水深(cm) | ||||
| 上部 | 下部 | 上部 | 下部 | ||||||
| 勾配1/100 Cシリーズ | C-1 | 6018 | 6018 | 6018 | 1分間 2分間 3分間 5分間 |
5 4.2 5 5.1 |
3.8 4.7 5 4.9 |
4.3 4.2 4 4.2 |
3.3 3 3 2.9 |
| C-2 | 4573 | 3754 | 819 | 1分間 2分間 3分間 5分間 |
3.8 3.9 4 3.9 |
3.8 4.1 4.1 3.8 |
3.5 3.5 3.3 3.2 |
2.2 2.4 2.3 2.2 |
|
| C-3 | 1851 | 1431 | 420 | 1分間 2分間 3分間 5分間 |
2.8 2.7 2.6 2.7 |
2.9 2.9 2.8 2.8 |
2.6 2.1 2.1 2.1 |
1.8 1.9 2 1.8 |
|
| C-4 | 1096 | 694 | 402 | 1分間 2分間 3分間 5分間 |
1.5 2 2 2.1 |
1.7 1.7 1.7 1.9 |
1.8 1.8 1.9 1.9 |
2.5 2.6 2.7 2.8 |
|
| 勾配1/300 Dシリーズ | D-1 | 872 | 620 | 252 | 1分間 2分間 3分間 5分間 |
1.8 2.2 2.1 2 |
2.8 2 1.9 1.9 |
1.9 2 2.1 2 |
1.4 1.6 1.9 1.6 |
| D-2 | 1176 | 899 | 277 | 1分間 2分間 3分間 5分間 |
2 2.4 2.3 2.1 |
2.2 2.5 2.5 2.1 |
2.3 2.3 2.3 2.4 |
2.3 2.3 2.3 2.2 |
|
| D-3 | 5736 | 4816 | 920 | 1分間 2分間 3分間 5分間 |
4.9 4.8 4.6 4.8 |
4.5 4.6 4.1 4.2 |
4 4.2 4.2 4.1 |
3.5 3.7 3.7 3.7 |
|
| D-4 | 5447 | 4500 | 947 | 1分間 2分間 3分間 5分間 |
4.5 4.5 4.6 4.7 |
4.6 4.6 4.8 4.8 |
4 4 4 4 |
3 3 2.8 2.8 |
|
表-1.2 土砂を含んだ氾濫流の実験条件一覧
 |
|
| (a) C-4 1分後 | (b) C-4 5分後 |
 |
|
| (c) C-1 1分後 | (d) C-1 5分後 |
(Cシリーズ 1/100)
 |
|
| (a) D-1 1分後 | (b) D-1 5分後 |
 |
|
| (c) D-3 1分後 | (d) D-3 5分後 |
(Dシリーズ 1/300)
 |
|
| (a) 1/100 流量小 (C-1 5分後) |
(a) 1/100 流量大 (C-1 5分後) |
 |
|
| (c) 1/300 流量小 (D-2 5分後) |
(d) 1/300 流量大 (D-3 5分後) |
勾配の違いによる堆積形状の細かな違いを図-1.10で調べてみる。同図では(a),(b)が勾配1/100、(c),(d)が勾配1/300で、左側(a),(c)が流量約1100cm3/s、右側(b),(d)が流量約600cm3/sのものを示している。前述したように、勾配の違いによる堆積形状の違いは顕著ではないが、勾配が緩やかな場合の方が最大堆積高の生じる位置がやや上流で本川からやや遠ざかった位置となる。この理由は、勾配が緩やかなほど、氾濫流が横方向に流れるようになるためであると考えられる。
図-1.11は砂の堆積の進行に伴って表面流がどのように変化するかを、発泡スチロール球の軌跡から読み取ったものである。通水開始から1分後では、堆積の高さは極めて低いため土砂を含まない氾濫流と同様で、流れの直進性が強く、比較的下流向きとなっている。これに対して、堆積高が高くなってくると、高い方向への流れが阻害されるのと、山を越えた流れは最急勾配方向に重力を受けるようになるため、流れの方向は横断方向にも向くようになる。
1.4 おわりに
今回の実験では、装置が小さいこともあって、実河川を意識した相似模型とはなり得なかった。今後は、大規模な水理模型実験と、土砂を含む氾濫流の数値解析が望まれる。
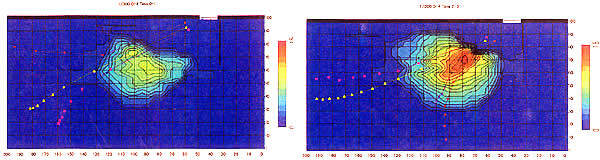 |
|
| (a) 1分後 | (b) 2分後 |
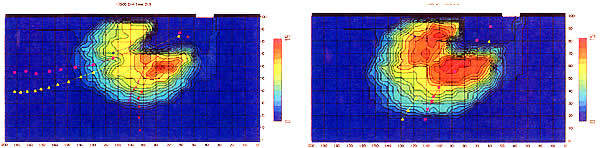 |
|
| (c) 3分後 | (d) 5分後 |
| 図-1.11 堆積形状と表面流向の変化 | |
参考文献
- 水理公式集、昭和60年版、pp. 283-296, 1985.
- 永嶋・田村・福岡ら:横越流堰の流量計数に及ぼす水面形の影響、土木学会年次学術講演会概要集第2部、pp. 208-209, 1999.
- 平田・須田・竹本:パソコンによる数値計算、pp. 69-72, 1982, 朝倉書店.
- 安達・高橋ら:急勾配水路の氾濫流とこれに起因する土砂堆積に関する実験、平成11年度金沢工業大学土木工学科工学設計IIIプロジェクトレポート、2000. 3.